Day 2 Task 2: 渋滞 (Traffic Congestion)

カナダは広い国である．しかし国土の多くは人が住まない地域であり，人口は南の国境付近に集中している．1962 年に造られたトランスカナダハイウェイは，東のセントジョーンズから西のビクトリアまで，距離にして 7 821 km となるこの細長い地域に住む人々を結んでいる．

カナダ人はホッケーが好きである．ホッケーの試合が終わると何千人ものホッケーファンが試合が行われた競技場から家まで車で移動するため，道ではひどい渋滞が発生してしまう．とある富豪はホッケーチームを買収し，ホッケーの競技場 (arena) を作りたいと思っている．あなたの仕事はホッケーの試合終了後に発生する渋滞の度合いを最小化するような競技場の設置場所を探し出し，彼を手助けすることである．

この国では道路網で都市が繋がれている．すべての道は双方向に移動可能である．任意の 2 つの都市の間にはちょうど 1 通りの 経路 がある．都市 c0 と ck の間に 経路 があるというのは，すべての i について，都市 ci-1 と都市 ci の間が道で繋がれているような異なる都市の列 c0, ..., ck が存在するということである．新しい競技場はただ 1 つの都市に建てられる．この新しい競技場が建てられる都市を競技都市 (arena city) と呼ぶこととする．ホッケーの試合終了後，競技都市以外に住むすべてのホッケーファンは競技都市から家まで移動する．各々の道の渋滞の度合いはその道を通るホッケーファンの数に比例する．あなたは，競技都市とした場合に最も渋滞する道の渋滞の度合いを最小化するような都市を探し出さなければならない．ただし，そのような都市の候補が複数ある場合，いずれの候補を解答しても良い．

プロシージャー LocateCentre(N,P,S,D) を実装せよ． N は都市の数を表す正の整数である．都市は 0 から N-1 までの番号を付けられている． P は N 個の正の整数の配列であり，各々の i について P[i] は i 番目の都市に住むホッケーファンの数を表す．すべての都市のホッケーファンの数の合計は 2 000 000 000 以下である． S と D はそれぞれ，道の位置を表す N-1 個の整数の配列である．各々の i について，S[i] と D[i] の 2 つの都市を結ぶ道があることを表す．プロシージャーは競技都市の候補である都市の番号を返す必要がある．

例

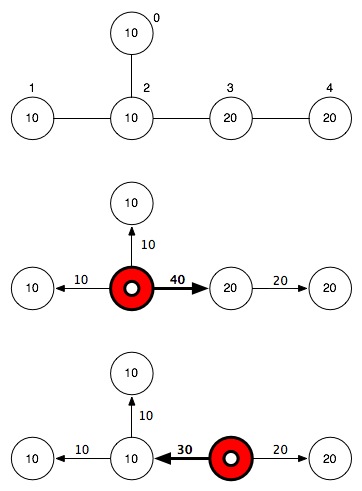例として，右図の上の 5 つの都市からなるネットワークについて考える．都市 0, 1, 2 のホッケーファンの数は 10 であり，都市 3, 4 のホッケーファンの数は 20 である．真ん中の図は都市 2 に競技場を建てた時の渋滞の様子を示しており，渋滞の度合いが最大となる道は太い矢印で示した道であり渋滞の度合いは 40 である．下の図は都市 3 に競技場を建てた場合の渋滞の様子を示しており，渋滞の度合いが最大となる道は太い矢印で示した道であり渋滞の度合いは 30 である．よって新しい競技場は都市 2 に建てるよりも都市 3 に建てる方が良いことがわかる．この例の入力データは grader.in.3a で与えられている．

注意

与えられた制約下で，小課題 3 を正解し，小課題 2 は不正解となる解答を提出することも可能であることをここで断っておく．ただし，最終的な課題全体の点数は ただ 1 つ の提出解答プログラムによって決まることにも注意せよ．

小課題 1 [25 点]

すべての都市が東から西へ一直線上に並んでおり，すべての道はその直線に沿って存在し分岐は存在しない． さらに各々の i (0 ≤ i ≤ N-2) について S[i] = i, D[i] = i+1 が成立する．

都市の数は 1000 以下である．

小課題 2 [25 点]

小課題 1 と同様の条件であるが，都市の数は 1 000 000 以下である．

小課題 3 [25 点]

小課題 1 の条件はもはや成立しない．

都市の数は 1000 以下である．

小課題 4 [25 点]

小課題 1 の条件はもはや成立しない．

都市の数は 1 000 000 以下である．

実装の詳細