
International Olympiad in Informatics 2011
2011年7月22-29日, タイ, パタヤ
Day 1 競技課題
日本語版

|
International Olympiad in Informatics 2011 |
RACEバージョン: 1.3 |
パタヤ市は, IOIと共同で「国際競走オリンピック」 (International Olympiad in Racing (IOR)) 2011 を主催することになった. 主催者として, 競走が可能である最適なコースを見つける必要がある.
パタヤ (Pattaya) ‐ チョンブリ (Chonburi) の大都市圏には N 個の都市があり, N-1 本の高速道路網で結ばれている. 各高速道路は双方向に移動可能であり, 異なった都市を結び, その長さはキロメートル単位の整数値をとる. 加えて, どの 2 つの都市の間も「ちょうど 1 つ」の経路で結ばれている. 言い換えると, どの都市からどの都市へも, 同じ都市を 2 度訪れることなく移動することができる方法がちょうど 1 つ存在する.
IORには, コースの開始都市から終了都市までの経路の合計距離が「ちょうど」 K キロメートルでなければならないという規則がある. 言うまでもなく, 衝突を防ぐためにどの高速道路も(したがって, 都市も), 2 度以上コースに使われることはない. 交通の混乱を最小にするために, コースに含まれる高速道路の本数をできる限り少なくする必要がある.
次のパラメータを持つプロシージャー best_path(N, K, H, L) を実装せよ:
配列 H の全ての値が 0 以上 N-1 以下であり, 配列によって表現される高速道路は上記のように全ての都市を結んでいることを仮定して良い. また, 配列 L の全ての値が 0 以上 1 000 000 以下であると仮定して良い.
あなたのプロシージャーは長さがちょうど K の適切な競走コースの 「高速道路の最小本数」を返す必要がある. その様なコースが無い場合は, あなたのプロシージャーは -1 を返す必要がある.
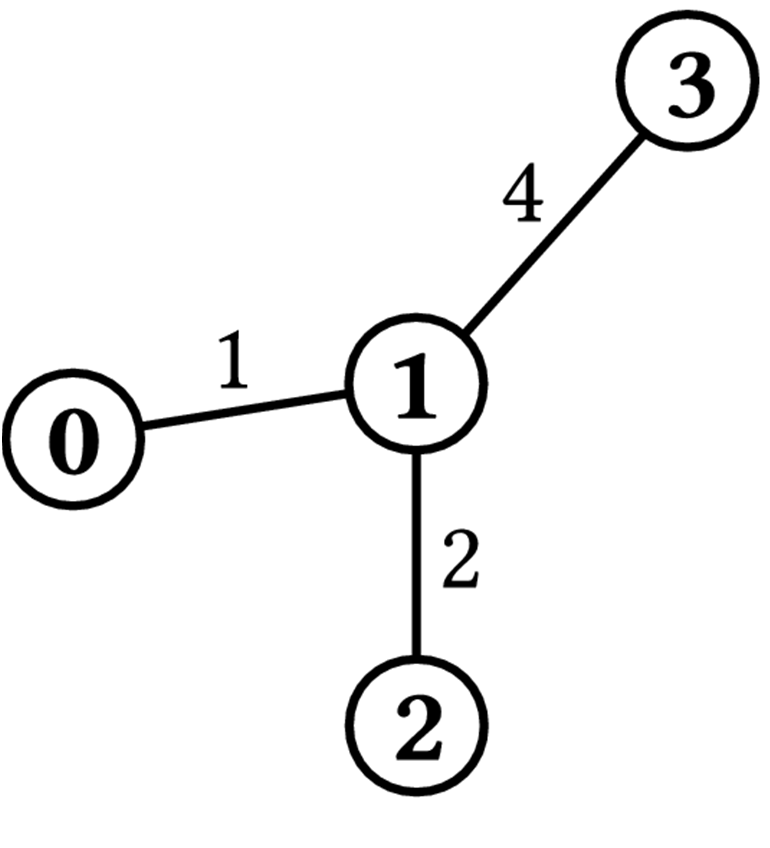
図 1
例として図 1 に示される N = 4, K = 3,
| H = | 0 | 1 | L = | 1 | ||
| 1 | 2 | 2 | ||||
| 1 | 3 | 4 |
の場合を考える.
この例では, コースは都市 0 から開始し, 都市1へ向かい, 都市 2 で終了する. このコースの長さはちょうど 1 km + 2 km = 3 km であり, 2 本の高速道路を含む. このコースは最適なコースであり, best_path(N, K, H, L) は 2 を返す必要がある.
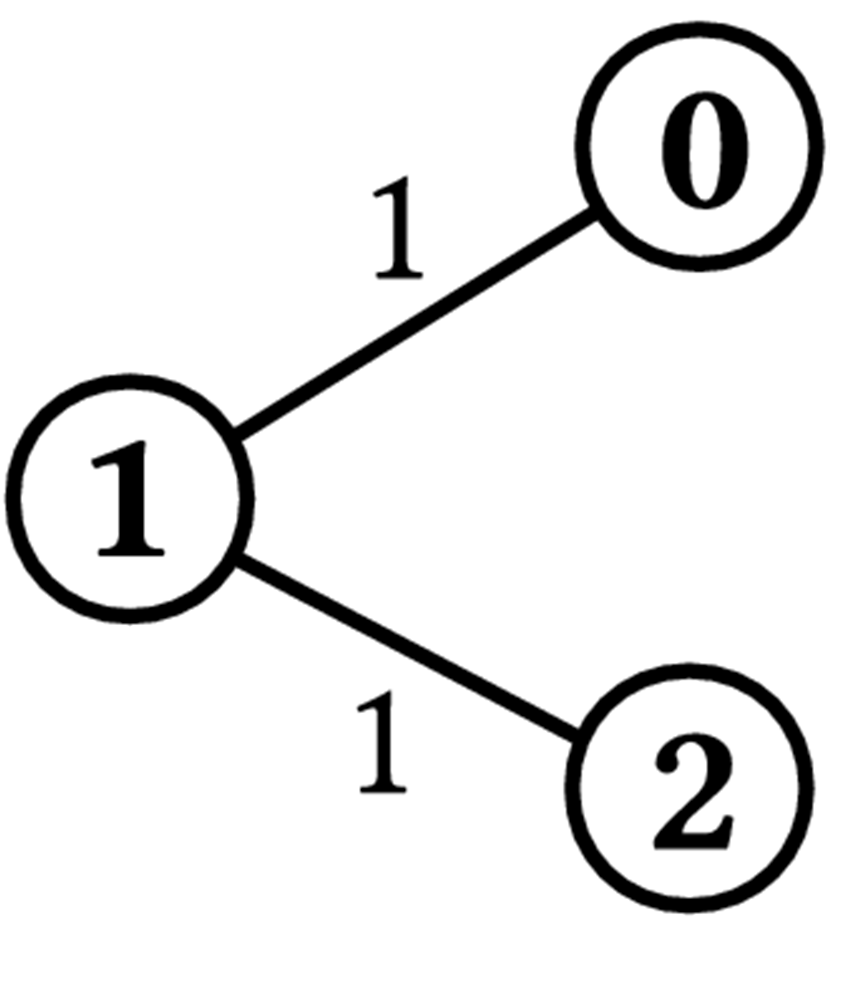
図 2
例として図 2 に示される N = 3, K = 3,
| H = | 0 | 1 | L = | 1 | ||
| 1 | 2 | 1 |
の場合を考える.
この例では, 適切なコースは存在しない.この場合 best_path(N, K, H, L) は -1 を返す必要がある.
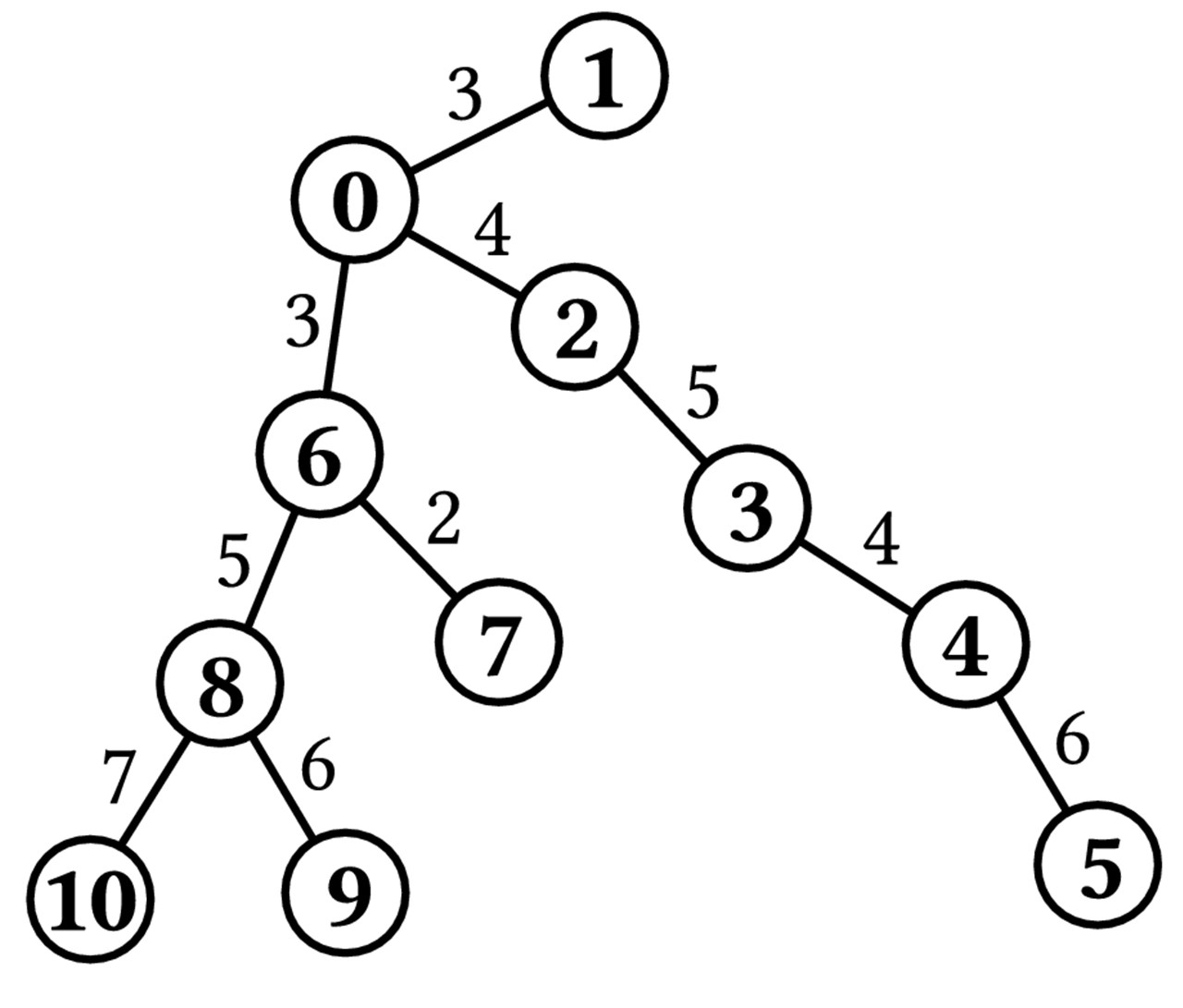
図 3
例として図 3 に示される N = 11, K = 12,
| H = | 0 | 1 | L = | 3 | ||
| 0 | 2 | 4 | ||||
| 2 | 3 | 5 | ||||
| 3 | 4 | 4 | ||||
| 4 | 5 | 6 | ||||
| 0 | 6 | 3 | ||||
| 6 | 7 | 2 | ||||
| 6 | 8 | 5 | ||||
| 8 | 9 | 6 | ||||
| 8 | 10 | 7 |
の場合を考える.
1 つの適切なコースでは, 都市 6 から都市 0 と都市 2 を経由し都市 3 に至る, 3 本の高速道路を含んでいる. 別のコースでは, 都市 10 から開始し都市 8 を経由し都市 6 に至る. 両方のコースの長さは要求通りちょうど 12 kmである. 1 本の高速道路からなる適切なコースは存在せず, 2 つ目のコースが最適である. したがって, best_path(N, K, H, L) は 2 を返す必要がある.
race/race.c または race.cpp または race.pasrace.h または race.pasrace.h または racelib.pasgrader.c または grader.cpp
または grader.pasgrader.in.1, grader.in.2,
...grader.expect.1, grader.expect.2,
...