
International Olympiad in Informatics 2011
2011年7月22-29日, タイ, パタヤ
Day 2 競技課題
日本語版

|
International Olympiad in Informatics 2011 |
CROCODILEバージョン: 1.3 |
考古学者の Benjamas は, 謎のワニの地下都市を探検していたが, 命の危険を感じ逃げることにした. 都市には N 個の部屋があり, M 本の双方向に通行可能な廊下で結ばれている. 各々の廊下は 2 つの異なる部屋を結んでおり, 結んでいる部屋の対はどの廊下についても異なる. 廊下ごとに, そこを通るための時間は異なるかもしれない. N 個の部屋のうち K 個の部屋は「出口の部屋」であり, 彼女はそこから脱出することができる. Benjamas は最初は部屋 0 におり, できる限り早く出口の部屋にたどり着きたい.
門番のワニは, Benjamas が脱出するのを防ぎたい. 彼は秘密のドアをコントロールし, 廊下を 1 本だけ封鎖することができる. つまり, 彼が新たに廊下を封鎖すると, その前に封鎖されていた廊下は再び通れるようになる.
Benjamas のおかれている状況を正確に記述すると次のようになる: 彼女が部屋から移動しようとすると, 門番はその部屋に接続する廊下のうち 1 本を選んで封鎖することができる. その後, Benjamas は封鎖されていない廊下のうち 1 本を選んでその先の部屋へ移動する. Benjamas が一度廊下に入ったら, 彼女が廊下を抜けるまで門番はその廊下を封鎖することはできない. Benjamas が次の部屋にたどり着けば, 門番はまた封鎖する廊下を選ぶことができる (Benjamas が直前に通った廊下でもよい).
彼女は単純な形の脱出計画をあらかじめ立てておきたいと思っている. より正確には, 部屋ごとに, そこにたどり着いたときに何をするかの指示を決めておこうと思っている. ある部屋 A について考える. A が出口の部屋ならそこから都市を脱出できるので, もちろん指示は必要ない. そうでない部屋については, 指示は次のいずれかの形でなければならない:
場合によっては, 門番は Benjamas が出口の部屋にたどり着くのを防ぐことができる (たとえば, 計画に従うと彼女が堂々巡りに入る場合などがそうである). Benjamas が門番の行動によらず必ず出口の部屋にたどり着くような計画を「良い」計画と呼ぶ. 良い計画に対し, T を「T 以下の時間で Benjamas が必ず出口の部屋にたどり着く」ような最小の値とする. この場合, その良い計画には「 T の時間がかかる」と言う.
次のパラメータをもつプロシージャー travel_plan(N, M, R, L, K, P) を実装せよ:
プロシージャーは, T の時間がかかる良い計画が存在するような最小の T を返さなければならない.
出口の部屋でない部屋には必ず 2 本以上の廊下が接続しているとしてよい.
また, T ≦
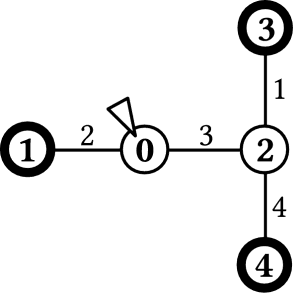
例として, 図 1 に示される N = 5, M = 4, K = 3,
| R = |
|
L = |
|
P = |
|
部屋は丸で表され, それらを結ぶ廊下は線で表されている. 出口の部屋は太線の丸で表されている. Benjamas は最初は三角のついた部屋 0 にいる. 以下の計画は最適な計画のひとつである:
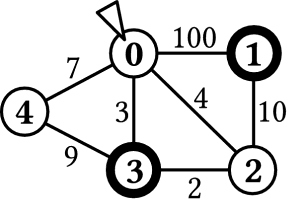
例として, 図 2 に示される N = 5, M = 7, K = 2,
| R = |
|
L = |
|
P = |
|
以下の計画は最適な計画のひとつである:
Benjamas は 14 単位時間以内に出口の部屋にたどり着く. よって, travel_plan は 14 を返さなければならない.
crocodile/
crocodile.c または crocodile.cpp または crocodile.pas
crocodile.h または crocodile.pasgrader.c または grader.cpp または grader.pasgrader.in.1, grader.in.2, ...grader.expect.1, grader.expect.2, ...