
| 第19回日本情報オリンピック 二次予選 |
 |
|
2019年12月12日
情報オリンピック日本委員会
|
小課題 1 では `?' の個数が 8 個以下であることがわかる.単純な解法として,`?' に `R', `S', `P' のどれを割り当てるかすべての場合を考え (最大 38 = 6561 通り),それぞれについて式を計算するという方法が考えられる.割り当てをすべて試すのは,再帰関数を用いたり,0 以上 3(`?' の個数) 未満の整数を対応させたりといった実装方法がある.問題となるのは式の計算の方法,すなわち構文解析である.様々な構文解析の方法のうち,ここでは 2 つを紹介する.
文字列中の区間についての動的計画法を用いて構文解析を行うことができる.これは与えられた BNF をそのままの形で用いる方法である.
文字列 E の i 文字目から j 文字目までの部分文字列について,以下の 4 つの値を保持する:
例えば,部分文字列 R+S に対してはこれらは順に false, true, true, `R' となる.これらの値は,区間の長さが短い順に埋めていくことで計算できる.例えば,i 文字目から j 文字目までが <term> であるのは,それが <factor> であるか,ある k (i < k < j) が存在して「i 文字目から k − 1 文字目までが <term> である」「k 文字目が `*'」「k + 1 文字目から j 文字目までが <term>」を満たす場合である.
計算すべき値が O(N2) 個あり,それぞれの計算が O(N) 時間でできるので,構文解析にかかる時間計算量は O(N3) となる.
本問の文法を言い換えると,
であることがわかる.このことを用いると,文字列のある位置から <factor> を読む処理ができれば,文字列のある位置からできるだけ長い <term> を読む処理ができ,それを用いて文字列のある位置からできるだけ長い <expression> を読む処理ができる.<factor> を読む処理は `(' を見た場合にそこから <expression> を読むことになるので,3 つの関数を用いた相互再帰で書ける.疑似コードは以下のようになる:
function expression():
value := term()
while 次の文字が '+' または '-':
1 文字読み進める
value := value + term() または value - term()
return value
function term():
value = factor()
while 次の文字が '*':
1 文字読み進める
value := value * factor()
return value
function factor():
if 次の文字が 'R' または 'S' または 'P':
1 文字読み進める
return 'R' または 'S' または 'P'
else:
1 文字読み進める (開き括弧)
value := expression()
1 文字読み進める (閉じ括弧)
return value
文字列の「今見ている場所」を管理し (具体的には,グローバル変数や戻り値などを用いて実装する),関数 expression, term, factor はそれぞれ今見ている場所からできるだけ長い <expression>, <term>, <factor> を読み,見ている場所を進め,計算結果を返す関数になっている.最初に文字列の先頭を見ている状態で関数 expression を呼ぶことで,式の計算結果がわかる (構文にエラーがなければ見ている場所は文字列の末尾となる).
このようなアルゴリズムは再帰下降法と呼ばれる.文字列の各位置を読む回数が expression, term, factor のそれぞれにおいて高々 1 回ずつであるから,時間計算量は O(N) である.再帰の深さも (よって空間計算量も) O(N) である.
`?' への割り当てをすべて試さずに答えを求めるためには,動的計画法の考え方が必要である.文字列 E の部分文字列として表される式のそれぞれについて,計算結果が `R', `S', `P' になるような割り当て方が何通りあるかをそれぞれ求める.そのような式同士に `+', `-', `*' の演算を行ったものについても計算結果ごとに割り当て方が何通りあるか求めることができる.
この考え方は以下の図のように表すことができる (入力例 1 に対応している).このような木は構文木と呼ばれる.
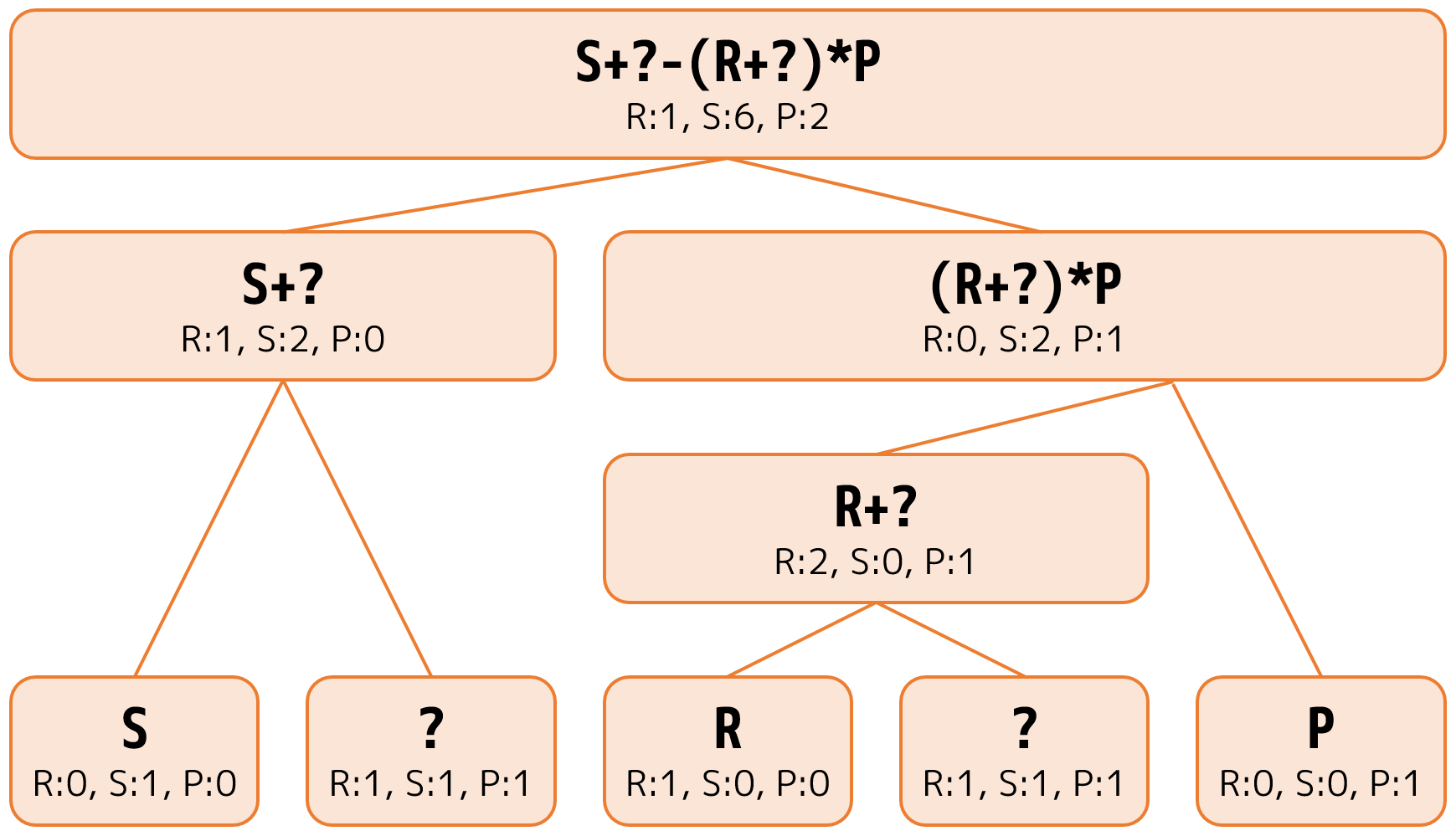
例えば,式 `S+?' の計算結果を `R', `S', `P' にする方法はそれぞれ 1 通り,2 通り,0 通りであり,式 (R+?)*P の計算結果を `R', `S', `P' にする方法はそれぞれ 0 通り,2 通り,1 通りである.これらに演算 `-' を行うと,S-S = S となるのが 2 × 2 = 4 通り,S-P = P となるのが 2 × 1 = 2 通りというように,式 S+?-(R+?)*P の計算結果を `R', `S', `P' にする方法が 9 回の掛け算でわかる.
この方法を,動的計画法による構文解析にそのままあてはめる (計算結果の代わりに何通りかを求めていく) と,O(N3) 時間でこの問題が解ける (小課題 2).
`R', `S', `P' を値とする計算の代わりに,「割り当て方が何通りかを表す整数の 3 つ組」を値に持つ計算をすると考えると,再帰下降法などによってO(N) 時間でこの問題が解ける (小課題 3).