
| 第20回日本情報オリンピック 一次予選(第2回) |
 |
|
2020年10月30日
情報オリンピック日本委員会
|
この課題には様々な解法が存在する.
問題文には,3 つの整数の組 (i, j, k) が満たすべき条件が記載されている.したがって,3 重ループを用いて,i, j, k を 1 から N の範囲で動かし,それぞれ条件を満たすか判定すればよい.
疑似コードを示す:

この解法の時間計算量は O(N3) である.(つまり,計算時間が N3 に比例する.)
解法 1 では,i の候補として 1 から N のすべてを試した.実はこの課題において,i として考慮すべきなのは,S に含まれる最初の `I` のインデックスのみである.
2 番目以降に出てくる `I` のインデックスを i として用いる組 (i, j, k) が条件を満たすならば,i だけを最初の `I` のインデックスに変えても,やはり条件を満たすからである.

同様に,j として考慮すべきなのは,S の i 番目より後ろに含まれる最初の `O` のインデックスのみである.k として考慮すべきなのは,S の j 番目より後ろに含まれる最初の `I` のインデックスのみである.
よって,文字列 S を先頭から順に調べ,
というアルゴリズムが成り立つ.
この解法の時間計算量は O(N) である.
解答例(C++) はこの解法 2 を実装している.
一部の言語では,正規表現を用いて文字列を処理できる.例えば,文字列 S がパターン `.*I.*O.*I.*` に一致するか判定することで,この課題を解くことができる.
解答例(Python,別解) はこの解法 3 を実装している.
ただし,一般に正規表現マッチングはバックトラック法 (バックトラッキング) を用いて実装されており,最悪の場合,時間計算量が文字列の長さについての指数関数時間になりうるため,注意が必要である.
解答例の実装であれば,時間計算量は O(N3) である.参考として,ある整数 N に対し,`I` を N 個,`O` を N 個,`A` を N 個並べた長さ 3N の文字列を引数とした場合の `re.fullmatch` の処理時間を両対数グラフで示す.
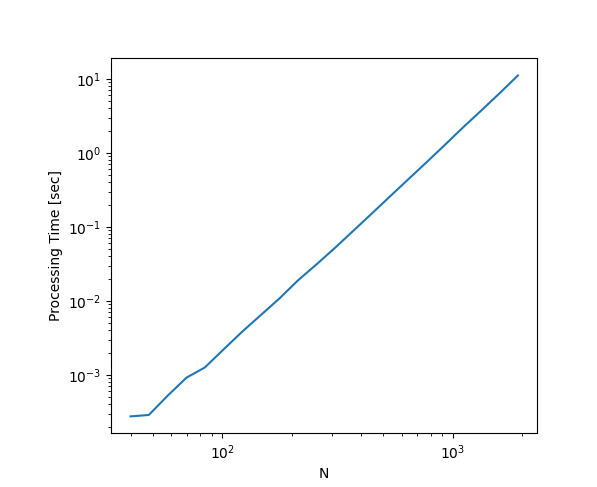
両対数グラフにおける傾きがおよそ 3 になっていることが読み取れ,確かに時間計算量は O(N3) である.
中川 みなみ,南出 靖彦『バックトラックによる正規表現マッチングの時間計算量解析』,情報処理学会論文誌プログラミング(PRO),Vol.9,No.2,p.28,2016. http://id.nii.ac.jp/1001/00163695/